Geoguessr用のドリル。
贈与経済2.0の話
贈与経済2.0というプロジェクトを知ったので、その可能性について考えていきたい。
それは何?
贈与経済2.0とは、旧来の贈与経済システムを改善したものであり、現在の資本主義システムの代替として取り組まれているものである。
問題の著書がこちら。現在はトヨタ財団の支援のもと実証実験を行っているとのことであり、絵空事というわけでもないらしい。その辺のユートピア思想とは一味違いそうだ。
資本主義には色々と不満があるものの、それに代わるものを作り出すのは極めて難しい。私はこういう思想を見ると心が躍ってしまうが、冷静に分析をしよう。
旧来の贈与経済
原始的な贈与経済は、日常の中でも観察することができる。
街で見知らぬ人に親切にしてあげたり、お世話になった人にご馳走したり、という営みが贈与にあたる。ここでの贈与とは、返礼を明示的に期待することなく、他者に能動的かつ一方的に奉仕すること、と言えるだろう。贈与した者は返礼を受け取れるとは限らないが、贈与の実績が信用として蓄積されて社会に通用する。これがインセンティブとなるわけだ。
しかし、これをそのまま現代社会の基幹システムとするには問題が多い。
まず、人間関係の問題だ。自分が贈与した実績は関係者の記憶に刻印される。これにより、発言力の大きい人物に奉仕したほうが有利な信用が得られることになってしまう。また、人間関係の断絶は贈与実績の消失を意味するため、中世並みに人間関係に束縛されることになってしまう。
もうひとつに、贈与実績の曖昧さがある。ある人物から頻繁にご馳走になるという日々が続くと、その人物との関係性は「お世話になった人」という曖昧な関係に昇華される。その曖昧さが、一生をかけても返礼しきれない負債となってのしかかり、実際の贈与実績以上の返礼を求められる上下関係を構築してしまう危険性がある。
贈与経済2.0が期待するもの
この問題に対処するために、当プロジェクトでは、贈与の実績をブロックチェーン上に記録することが試みられている。
誰がどんな贈与をしたかを第三者が確認することができるため、人間関係が切れても贈与実績が消失することがない。また、贈与の実績をさかのぼって確認することができるため、曖昧な上下関係の持続に歯止めをかけることができるというわけだ。
では、現在の社会に贈与経済2.0を導入することで、何が期待されるのか。
ひとつには、スタートラインの平等だ。資本主義社会における資産に相当するものは贈与の実績になるであろうが、贈与経済2.0では、これらを相続することはできない。実績は個人のアカウントに紐づいているため、親と子は完全に独立した主体として扱われる。これが生まれによる資本の格差の緩和につながるのだという。
もうひとつには、過剰生産や環境破壊、ブルシットジョブといった、資本主義社会特有とされる問題の解消がある。贈与はコミュニティ内の人に狭く行われるという性質上、過剰に生産したり役に立たない仕事が生じたりする可能性が少なくなるのだという。
次世代システムとしての可能性
では、贈与経済2.0は資本主義のオルタナティブとなるのだろうか。私は、全くの代用品とはならないと考える。それは3つの理由による。
ひとつには、資本主義プロセスを禁止することができない点にある。近代的な所有権を採用している限り、合理化の末に資本主義が生じることは必至である。所有があれば物々交換が生じ、物々交換が生じれば商品貨幣が生じる。贈与経済2.0が導入されても資本主義プロセスが裏で動くことを止められない。
ふたつめに、物資の入手が保証されない点だ。どれだけ世界中の人に品物を届けたとしても、明日の食糧がもらえる保証はない。農家は野菜を100人に与えても90人に与えても信用に大差はないからである。ましてや、評判の悪い人に食糧を与えた記録が汚点として意味づけをされるのだとしたら、特定の人を飢えさせるインセンティブすら働きうる。
最後に、そもそも資本主義社会の問題点が解消されないという点だ。贈与経済2.0においても、大量生産は少ない労力で多くの贈与ができる手段として合理的に機能する。遠方の産物や贅沢品にありつきたいという欲望が生じれば、それを叶えることは十分に動機づけられる。資本主義社会の問題の多くは資本主義によってではなく、大規模システムに発展したことで生じるものである。贈与経済2.0もシステマティックに成熟すれば同様の問題を引き起こしうる、と私は考える。
このように、贈与経済2.0が単独で社会を担っていくのは難しいと考える。しかしながら、贈与経済2.0が資本主義にはない視点をもたらすのは確かであろう。世界が資本主義と贈与主義の両輪で回っていくようになれば非常に面白い。
【自分用】国旗クイズ
最近国旗を忘れつつあるので、復習用に。
【将棋AI】KIF→SFEN 変換プログラムを作った
経緯
今週から将棋AI作りを始めた。以前も取り組んでいた時期があったのだが、将棋盤GUIとの連携などでしんどくなってやめてしまった。
学習データを準備するべくデータベース(Shogi DB2 - 無料の棋譜サービス 将棋DB2)を見てみると、将棋AI界で標準とされているSFEN形式でダウンロードできないではないか。仕方がないので、KIF形式からSFEN形式への変換プログラムを作成した。
概要
要するに、「1 2六歩(27) (00:00/00:00:00)」→「2g2f」の変換を行う。
実装はC#で行った。Visual Basicなどをインストールすればすぐにビルドができるので、よければ使ってみてほしい。
ネットに公開したときに便利だろうと、最初はPowershellで作ろうと思っていた。しかし、意外と複雑な処理が求められたためC#に切り替えた。
ソースコードは長いので最後に載せる。
使い方
アプリを任意のフォルダに配置し、そのフォルダでコマンドプロンプトを開く。
コマンドプロンプト上で "KIF2SFEN > test.txt" を実行する。
アプリ実行中になると、こんな画面がでる。
棋譜を貼り付ける前に "s" と一文字打って実行(Enter)する。これによって、出力テキストファイルに "startpos" という文字が出力されるので、対局開始の表示になる。

将棋DB2(Shogi DB2 - 無料の棋譜サービス 将棋DB2)からKIF形式のソースコードをコピーし、そのまま貼り付けてEnterキーを押す。
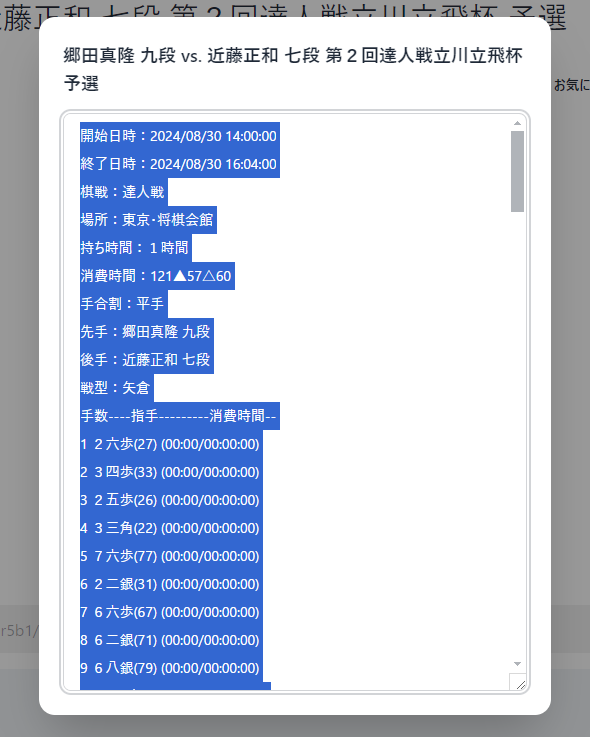
続けて棋譜を入力したいときには、"s"コマンドを実行していったん区切ってから、次の棋譜を入力する。
使い終わったら"quit"コマンドでアプリを終了できる。
![]()
同じフォルダに出力されている test.txt を見てみると、棋譜がSFEN形式で出力されている。

コマンド一覧
- s : "startpos"を結果に出力する。棋譜と棋譜の間にはこれを実行して区切る。
- KIF表現 : 将棋DB2の表現に則り、先頭が数字である文字列をこれと認識する。
- quit : アプリを終了する。
- その他 : 上記以外の文字列はすべて無視される。
なぜKIF形式なのか
将棋DB2はKIF形式のほかにもCSA形式とKI2形式に対応している。これらの中からKIF形式を選んだ理由も記載しておく。
KIF形式で最も処理上優れていると思ったのは、駒打ちを明示してくれるところである。6五に移動できる銀があったとしても、「6五銀打」と表現してくれる。また、移動前の駒の位置を明示してくれる点も、SFENと通ずる。
ソースコード
using System;
using System.Collections.Generic;
using System.Globalization;
using System.Linq;
using System.Security.Cryptography;
using System.Text;
using System.Threading.Tasks;
using System.Xml.XPath;
using System.Text.RegularExpressions;
namespace KIF2SFEN
{
internal class Program
{
static void Main(string[] args)
{
string cmd;
// "同○○"の記法に対応するためループ外で定義
int destX = 0; //駒移動の終点X(1~9)
int destY = 0; //駒移動の終点Y(1~9)
while ((cmd = Console.ReadLine()) != null)
{
string[] kif = cmd.Split(' '); // KIFコマンド
// アプリを終了するコマンド
if (cmd == "quit")
{
break;
}
// 対局同士を区切るためのコマンド
else if (cmd == "s")
{
Console.WriteLine("startpos");
}
// メインとなる変換処理
// 先頭が数字でない行は無視する
else if (Regex.IsMatch(kif[0], @"^\d+$"))
{
int originX = 0; //駒移動の起点X(1~9)
int originY = 0; //駒移動の起点Y(1~9)
char piece = ' '; // 駒種
Boolean isPromoted; // 成り移動の場合のみTRUE
string result = ""; // 結果
// 投了の場合
if (kif[1] == "投了")
{
result = "resign";
}
// 駒打ちの場合
else if (kif[1].Contains("打"))
{
// 先手番の場合
if (int.Parse(kif[0]) % 2 == 1)
{
// 打たれた駒種の判別
string koma = new StringInfo(kif[1]).SubstringByTextElements(2, 1);
switch (koma)
{
case "歩":
piece = 'P'; break;
case "香":
piece = 'L'; break;
case "桂":
piece = 'N'; break;
case "銀":
piece = 'S'; break;
case "金":
piece = 'G'; break;
case "角":
piece = 'B'; break;
case "飛":
piece = 'R'; break;
}
}
// 後手番の場合
else
{
// 打たれた駒種の判別
string koma = new StringInfo(kif[1]).SubstringByTextElements(2, 1);
switch (koma)
{
case "歩":
piece = 'p'; break;
case "香":
piece = 'l'; break;
case "桂":
piece = 'n'; break;
case "銀":
piece = 's'; break;
case "金":
piece = 'g'; break;
case "角":
piece = 'b'; break;
case "飛":
piece = 'r'; break;
}
}
// 打たれた場所の特定
string firstChar = new StringInfo(kif[1]).SubstringByTextElements(0, 1);
string secondChar = new StringInfo(kif[1]).SubstringByTextElements(1, 1);
// 1文字目はそのまま数字に変換する
switch (firstChar)
{
case "1":
destX = 1; break;
case "2":
destX = 2; break;
case "3":
destX = 3; break;
case "4":
destX = 4; break;
case "5":
destX = 5; break;
case "6":
destX = 6; break;
case "7":
destX = 7; break;
case "8":
destX = 8; break;
case "9":
destX = 9; break;
}
// 2文字目の漢数字部分を変換する
switch (secondChar)
{
case "一":
destY = 1; break;
case "二":
destY = 2; break;
case "三":
destY = 3; break;
case "四":
destY = 4; break;
case "五":
destY = 5; break;
case "六":
destY = 6; break;
case "七":
destY = 7; break;
case "八":
destY = 8; break;
case "九":
destY = 9; break;
}
// 結果文字列の組み立て
result = piece.ToString() + "*" + destX.ToString() + ((char)(destY + 'a' - 1)).ToString();
}
// 駒移動の処理
else
{
// "同○○"でない場合は移動先を更新する
if (!kif[1].Contains("同"))
{
string firstChar = new StringInfo(kif[1]).SubstringByTextElements(0, 1);
string secondChar = new StringInfo(kif[1]).SubstringByTextElements(1, 1);
// 1文字目はそのまま数字に変換する
switch (firstChar)
{
case "1":
destX = 1; break;
case "2":
destX = 2; break;
case "3":
destX = 3; break;
case "4":
destX = 4; break;
case "5":
destX = 5; break;
case "6":
destX = 6; break;
case "7":
destX = 7; break;
case "8":
destX = 8; break;
case "9":
destX = 9; break;
}
// 2文字目の漢数字部分を変換する
switch (secondChar)
{
case "一":
destY = 1; break;
case "二":
destY = 2; break;
case "三":
destY = 3; break;
case "四":
destY = 4; break;
case "五":
destY = 5; break;
case "六":
destY = 6; break;
case "七":
destY = 7; break;
case "八":
destY = 8; break;
case "九":
destY = 9; break;
}
}
// 移動元の読み取り
int index = kif[1].IndexOf('(') + 1;
originX = kif[1][index] - '0';
originY = kif[1][index + 1] - '0';
// 成り移動かどうかを取得
isPromoted = new StringInfo(kif[1]).SubstringByTextElements(3, 1) == "成";
// 結果文字列の組み立て
result = originX.ToString() + ((char)(originY + 'a' - 1)).ToString() + destX.ToString() + ((char)(destY + 'a' - 1)).ToString() + (isPromoted ? "+" : "");
}
// 結果文字列の出力
Console.WriteLine(result);
}
}
}
}
}
言語活動としての倫理的判断
倫理学の書籍を読んでいると、どうも、「倫理」というものが特別視されすぎているという印象を受ける。倫理的判断は何ら特別な哲学的判断なのではなく、普通の言語活動の一環だと思っている。そういう視点からメタ倫理学的な考え事を書いていきたい。メタ倫理学と呼ぶことすら仰々しい。そう呼ばれているものの一部は、単に言語活動一般として分析されれば事足りるのではないか。
倫理的判断ないし倫理的な発言とは、「善い」「悪い」「すべき」「それはダメでしょ」等の語群を使う発言だといえる。これらを「倫理的語彙」と呼ぼう。我々の倫理的判断の根拠や源泉をあたるためには、それら倫理的語彙の学習過程に着目する必要がある。我々は、倫理的語彙やその使用をどのように学んできたか?
私たちは、倫理的語彙の意味を教えられた後にその用例を学んだ、のではないはずだ(そういう言語化ができないことは、ムーアが「自然主義的誤謬」の名で示している)。実のところ、ある出来事とそれら倫理的語彙が使用されている場面とが一挙に、言語学習過程の我々に与えられてきたはずだ。つまり、それら倫理的語彙は、それらが言及しようとしている事例とともに示されるのが常であった。
そのとき、我々は単に語彙が使用されているのを見るだけであり、それが倫理的発言であるということすら明示されない。片付けをした直後に「えらいね」と発話され、別の園児を叩いた子に対し「ダメ」と発話される。そのような場面を幾度となく経験することで、私たちは「善い」「悪い」という語がそれぞれどんな場面に似つかわしいかを感じ取っていく。これが倫理的語彙、ひいては倫理の学習における実際の姿ではないだろうか。
このような学習は幼少期のみに見られるわけではない。我々は幼少期のうちに倫理的語彙を「学び終わる」のではないのだ。それら語彙は日常の言語活動において絶えず用いられ、事例は常に蓄積されていく。
そのような学習と同時に我々も、他の人の真似をして倫理的判断を下していく。ある種の場面や言動に対して、倫理的語彙を使うのだ。ここで考慮されるのは、類似する過去事例の存在と、そこで発揮された語彙の効力である。盗みを働こうとする人に対して「よくないよ」と発言することは、単に自然な発言だったというだけでなく、その盗みを抑止する効果も発揮してきたはずだ。私たちは、その語がその場に適合することを確信しつつ、その語彙が放つ効力にも期待して、その語を発するのである。中には「倫理的判断が難しい事柄」というものもあるが、それは類似する過去事例の不足を主張しているに過ぎない。
これが、倫理的判断がどのように下されているか、の現状だ。では、この説明によってメタ倫理学の探究に終止符が打たれるのかというと、それは全く違う。世の中であまり明示されないが、メタ倫理学はふたつのことを探求していると私は考えている。①我々は現状どのように倫理的判断を下しているのか、と、②我々は理想的にはどのように倫理的判断を下すべきなのか、である。今回述べたのは①に対する回答にすぎず、そこでの自分の立場を整理したものだ。今後は②についても何か言えたらいいなと思っている。
トランスエイジからトランスジェンダーを考える
最近、トランスエイジという概念が注目を集めている。トランスエイジとは、身体の年齢(戸籍上の年齢)と自認する年齢が異なる状態のことだ。トランスジェンダーが比較的世間から受け入れられつつあるのに対して、トランスエイジ概念はかなり批判を浴びているみたい。まあいろいろ言われているが、僕たち(年齢違和を感じるか否かにかかわらず)が問うべきことはひとつだ。
僕たちはトランスエイジという概念を認めるべきなのか?
そもそもだけど、新しい概念が提唱されているわけだ。既存観念では十分でなく、トランスエイジ概念が必要だとされた理由があるはずだ。ここで、オッカムの剃刀を応用した考え方をする。トランスエイジという概念を使用せずしてその問題を解決できるんなら、そのほうがシンプルでいいはず、ということだ。
本来であれば、そのあたりを踏まえて、トランスエイジ概念の必要性についてみんなで議論しよう!という話になる。でもここで問題がある。トランスエイジ概念の必要性は、年齢についての違和を感じる人間にしか経験できない、という壁だ。民族や宗教の問題においてもそうだけど、万人が経験できないということは対話において分断を生んでしまう。そして、対話ができないことをいいことに、雑多な概念が乱立してしまうこともある。もどかしいね。
現時点でトランスエイジについてこれ以上の深掘りは難しそう。 むしろこれを機に、すでに世間から認識されているトランスジェンダーについてもう一度考えてみたい。
トランスジェンダーとは、狭義には、身体性と性自認が異なる状態のこと。ここで重要なのは性自認という概念だな。ある見方をすれば、性自認とは、自分の望む扱われ方を性別の名で呼んだもののことだといえる。つまりそれは、性別によって扱われ方が変わるという前提に基づいている。ということは、世間が性別に関係なく人間を扱うようになってしまったら、性自認概念は根底から揺さぶられる。不思議な構造だなあ。
さて、性自認についてもオッカムの剃刀風に考えてみる。 性自認という概念を持ち出すことなく、世間での扱われ方を変えてもらうことができるなら、そのほうがシンプルでいいよねって話。しかし、思うに、今の世間は性別によって人間の扱い方を変えることをやめようとはしない。少なくとも、すぐに世間が変わることはなさそう。そういうことを踏まえると、既存の「性別」という概念の力を借りることによって自らの扱われ方を変えることができる「性自認」概念は、かなり理にかなっていて有用なアイテムだなあと感心する。(何様?)
ここで、「身体の性が本来の性別だ!」とか「性自認というのが真の性別なのだ!」などというのはどちらもナンセンスだ。なぜなら、ここで問題になっているのは「性という言葉をどのように用いることが良い社会に繋がるのか?」ということだからだ。
新しい概念が生み出されようとしているとき、そこには必ずプラグマティックな問いが生じる。生じなくてはならない。
モンテカルロ法で円周率を求める
モンテカルロ法で円周率を求めるやつを実装した。 プロットする点の数を入力してボタンを押すと、点がランダムに生成される。どれくらいの割合で円の内部に含まれたかを計算することにより、円周率を求めることができる。プロット数が大きいほど当然精度は上がるが、処理はクライアントサイドなので好きに決めてほしい。
プロット数:
計算結果: